Construct DFA | Number of a is Odd & Number of b is Not Divisible by 3

How to construct DFA to accept a language L={Strings in which the total number of ‘a’ is an odd and total number of b’s is not divisible by 3}?

This is a complicated question to construct DFA. To solve this kind of questions use divide and conquer strategy.

Steps to Construct DFA:

• Divide this problem into two parts.
  Construct the DFA for a string which has the total number of ‘a’ is odd.
  Construct the DFA for a string which has the total number of b’s is not divisible by 3.
• Once done, combine both the DFA automata.
• To get minimal DFA, remove any dead/unwanted/unreachable/duplicate state from the DFA.

Construct DFA for a string which has a total number of ‘a’ is odd:

This is a simple DFA with 2 states. One is starting state and other is the final state. It accepts all the string which have the occurrence of odd numbers of a.

There is no change in the transition state for the occurrence of b. So occurrence ob b forms the loop on the same state.

Construct DFA for a string which has a total number of ‘b’ is not divisible by 3:

To make it simple, follow these two steps

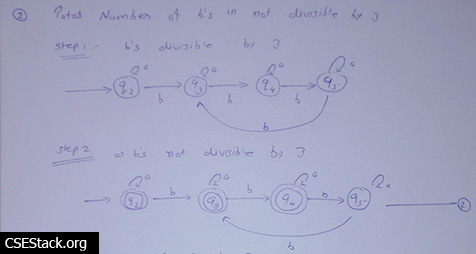
Step 1: construct DFA that accepts the string which has the total number of b’s is divisible by 3.

Step 2: Take the negation of constructed automata. This is possible by changing all the non-final states to final states and all final states to non-final states.

Construct Final DFA:

Combine both the above automata to construct DFA that accepts all the strings with the total number of ‘a’ is an odd & total number of b’s is not divisible by 3.

Take the combinations of all the states from both DFAs. So there are 8 states (4*2) which include 3 final states.

Find minimal DFA:

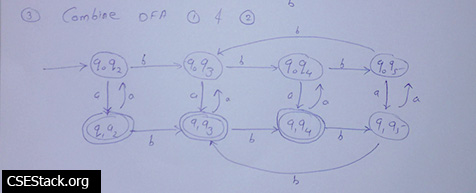
Remove all the unwanted stated from DFA. Unwanted states can be which are not reachable from starting state, a dead state which does not lead anywhere. Combine all the states that have all transitions to the same states.

In this case, there are not any unwanted states in DFA. Also, don’t have any common states to be combined.

This answer is elaborated based on the question asked in GATE CSE Facebook Community for GATE aspirants.

To construct DFA, it needs to practice. You can refer to the book Theory of Computation by Ullman to practice answering such kind of questions.

Note for GATE aspirants: If you are solving this question in GATE exam, it is time-consuming. In GATE, there are MCQ questions. There will be four answers with four DFA automata. Instead of constructing DFA, try to find out the answer by matching language given in the question with given automata in the answers.  (Reference: How to prepare for GATE)

Aniruddha Chaudhari

I am a Python enthusiast who loves Linux and Vim. I hold a Master of Computer Science degree from NIT Trichy and have 10 years of experience in the IT industry, focusing on the Software Development Lifecycle from Requirements Gathering, Design, Development to Deployment. I have worked at IBM, Ericsson, and NetApp, and I share my knowledge on CSEstack.org.