[Solved] Find Lowest Common Ancestor in the Binary Tree

In an earlier tutorial, we have seen

• what is the ancestor of a node in the binary tree?
• How to find and print all the ancestors of a given node in a Binary tree?

If you have not gone through it, read it here.

In this tutorial, we will find the lowest common ancestor in the binary tree when two nodes are given.

Let’s take the below binary tree example.

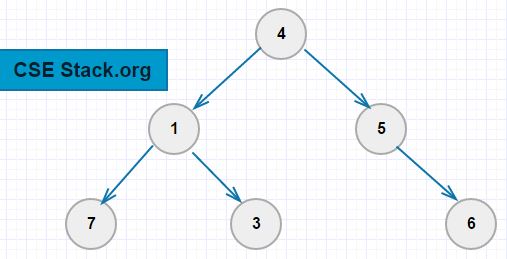
The node ‘x’ is the lowest common ancestor of given two nodes if two nodes present on either side (left and right) of ‘x’.

Example:

• The lowest common ancestor of nodes 7 and 3 is 1.
  Node 7 is present in the left branch and 3 is present in the right branch of node 1.
• The lowest common ancestor of nodes 3 and 6 is 4.
  Node 3 is present in the left branch and 6 is present in the right branch of node 4.

Algorithm to find the lowest common ancestor in the Binary Tree

Here is the simple algorithm to find the lowest common ancestors of two nodes (says ‘a’ and ‘b’) in a binary tree.

• Find all the ancestors of node ‘a’, save them in the list (says, ancestorsA)
• Find all the ancestors of node ‘b’., save them in the list (says, ancestorsB)
• Search for the first common node in the list ancestorsA and ancestorsB. This will give you the lowest common ancestor.

Example:

Let’s find the common ancestor of nodes 3 and 6.

• Ancestors of node 3: [1, 4]
• Ancestors of node 6: [5, 4]
• The first common element is ‘4’. So, the lowest common ancestor of nodes 3 and 6 is ‘4’.

Use this logic to write a code in any programming language you are comfortable with, like C/C++, Java, Python…

This problem was asked to me in one of the Amazon interview round.

Python Program

Here we are maintaining two list ancestorsA and ancestorsB to stores all the ancestors of two nodes nodeA and nodeB.

Code:

[python]
#binary tree node structure

ancestorsA=[]
ancestorsB=[]

class node:
def __init__(self, val, left=None, right=None):
self.left=left
self.val=val
self.right=right

#function to print all the ancestors of a given node
def findAncestors(root, val, listAncestors):
if not root:
return False
else:
if root.val==val:
return True
else:
if findAncestors(root.left,val, listAncestors) or \
findAncestors(root.right,val, listAncestors):
listAncestors.append(root.val)
return True

#create binary tree
root=node(4)
root.left=node(1)
root.right=node(5)
root.left.left=node(7)
root.left.right=node(3)
root.right.right=node(6)

nodeA=6
nodeB=3

findAncestors(root, nodeA, ancestorsA)
findAncestors(root, nodeB, ancestorsB)

for i in range(0, min(len(ancestorsA), len(ancestorsB))):
if ancestorsA[i]==ancestorsB[i]:
print("The lowest common ancestor in the binary tree \
for nodes %d and %d is %d." \
%(nodeA, nodeB, ancestorsA[i]))
[/python]

Output:

The lowest common ancestor in the binary tree for nodes 6 and 3 is 4.

Note: To find common ancestors, you don’t need to sort the nodes in a Binary tree. This solution works even if the nodes are in an unsorted order.

Complexity

To calculate the ancestors of any node in the binary tree takes the time of O(n).

A total number of ancestors to any node can not exceed log(n). In the worst case, it takes O(log(n)) to find the first common ancestor node.

So, the total complexity of this problem is O(n)+O(n)+O(log(n)) which is equivalent to O(n).

Aniruddha Chaudhari

I am a Python enthusiast who loves Linux and Vim. I hold a Master of Computer Science degree from NIT Trichy and have 10 years of experience in the IT industry, focusing on the Software Development Lifecycle from Requirements Gathering, Design, Development to Deployment. I have worked at IBM, Ericsson, and NetApp, and I share my knowledge on CSEstack.org.